






|
Optimization Problems
|



|
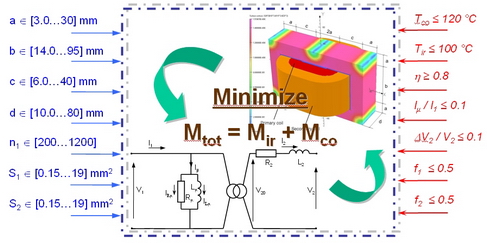
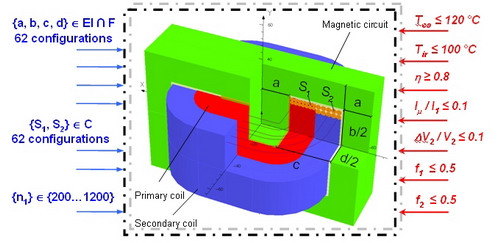
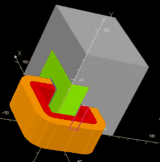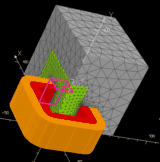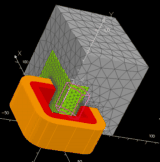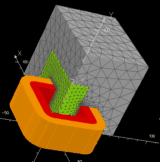
A. Combinatorial Optimization Problem The problem contains 7 discrete design variables. There are three parameters {a, b, c} for the shape of the lamination, one for the frame {d} (Fig. 2), two for the section of enamelled wires {S1, S2}, and one for the number of primary turn {n1}. There are 24 types of lamination from catalogue r.bourgois®, 62 combinations between the laminations EI and the frames from catalogue isolectra-martin®, and 62 types of enamelled wires from invex®. The number of primary turn n1 is integer but only 1,000 values are allowed, leading to 246,078,000 possible combinations. All the feasible values are given in the following files .
Fig. 2. Combinatorial Optimization Problem There are 7 inequality constraints applied on this problem. The copper and iron temperatures Tco, Tir respectively are less than 120°C and 100°C. The efficiency η is greater than 80%. The magnetizing current Iμ/I1 and drop voltage DV2/V2 are less than 10%. Finally, the filling factor of both coils f1, f2 is lower than 0.5. The objective function is to minimize the mass Mtot of iron and copper materials. B. Multi-Level Optimization Problem The multi-level continuous optimization problem aims to align a coarse model
Fig. 3. Multi-level Optimization Problem C. Multi-Objective Optimization Problem For the multi-objective optimization problem, one of seven constraints, e.g. the efficiency, may be changed to an objective in order to have a multi-objective optimization problem. Thus the multi-objective function is to minimize the total mass and maximize the efficiency.
|