Multi-Objective Optimization

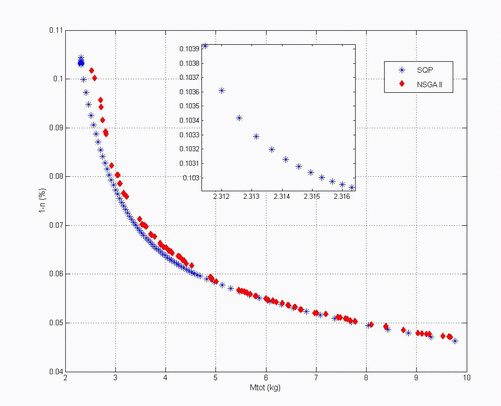
The multi-objective optimization problem of this benchmark has two conflicting objectives: minimize the total mass M_tot, and maximize the efficiency η . Two algorithms: Weighted Sum (WS) method using the Sequential Quadratic Programming (SQP) and Non-Dominated Sorting Genetic Algorithm (NSGA II) are tested with the continuous variables.

The most widely used method for multi-objective optimization, weighted sum method transforms biobjectives into a aggreated scalar objective function by multiplying both objective functions by a weighting factor varying in [0,1]. Thus, the suboptimization is normalized as:

       

 

Fig. 6 shows Pareto-optimal fronts of both methods with 100 points. The Pareto fronts of this problem are convex.

   

                Fig. 6. Paretos-optimal fronts of the multi-optimization found by WS and NSGA II

   

Introduction | Optimization Problems | Models | Comparison | Combinatorial Opt. | Multi-Level Opt. |

Multi-Objective Opt. | Your results