Optimization methods
|
Date |
30/05/2007 |
||
|
Author |
F. Moussouni, T. V. Tran, S.
Brisset, P. Brochet |
||
|
Affiliation |
L2EP
– EC Lille – France |
||
|
Email |
fouzia.moussouni@ec-lille.fr, tran.tuan-vu@ec-lille.fr, stephane.brisset@ec-lille.fr |
||
|
Method |
Genetic
Algorithm |
||
|
References |
[1] J. C. Spall, Introduction to stochastic search and
optimization, A John Wiley & Sons, Inc., Hoboken, New Jersy,
2003. [2] Z. Michalewicz, Genetic Algorithms + Data Structures =
Evolution Programs, ISBN 3-540-58090-5 |
||
|
Description of the method |
GA is a stochastic method based on the In the optimization of the safety
isolating transformer problem, each individual in the population is
considered as a combination of three chromosomes (Fig. 1). The genome encoding of the three chromosomes is a discrete value (Fig. 1).
Fig. 1. Genome encoding of chromosomes As the reproduction operators depend on the
encoding and on the problem [5],
specific crossover and mutation operators are implemented, in this study. At the new generation, the mutation operator
makes random changes on some individuals in order to jump outside local
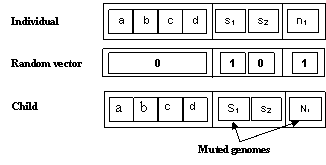
optima. In this study, a bit flip mutation is used. Bit lip mutation is a two-step process. First,
the algorithm creates a random binary vector, then, selects genes of an individual
for mutation, where the vector is a
Fig. 1. Bit flip mutation: Muted
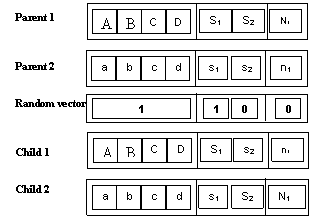
genomes are selected uniformly from the data base Crossover combines two parents, to form
children, for the next generation. Then a scattered crossover is used. This type of crossover creates
a random binary vector. So, the genes are selected from the first parent
where the vector is a 1, and from the second one where the vector is a 0, and
combines the genes to form the first child, and verse versa to form the
second one (see fig. 2).
Fig. 2. Scattered crossover: Parents are selected
uniformly from the data base For GA parameters, the following values are
used: population size N = 60, maximum number of generations T = 100,
crossover probability 0.9, binary tournament selection operator is used. If
the objective value is not improved over 50 generations the algorithm stops. As optimization of the safety
isolating transformer is a non-linear constrained problem the external
penalty approach is used. The objective function and non-linear constraints
are combined to formulate the following sub-problem:
Where f(X) = Mtot (X),
is the original objective function to be optimized, gi(X)
are the m=7 inequality constraints (see equation (1)). The parameter µ
is a penalty factor updated at each generation k as follow: a is a positive parameter set to 10.
µ0 is the upper limit of µ(k), given by the users
and must be positive and very large. |
||
|
Publication of the method |
|